小学校5年生の算数に「倍数・約数」という学習があります。
倍数や約数を探すときに知っていると便利なのが「素数」です。「1と自分自身しか約数を持たない数」ですね(1は除く)。
この素数を見つけるのに便利な方法が「エラトステネスのふるい」と呼ばれている方法です。
ふるいのやり方(素数の見つけ方)
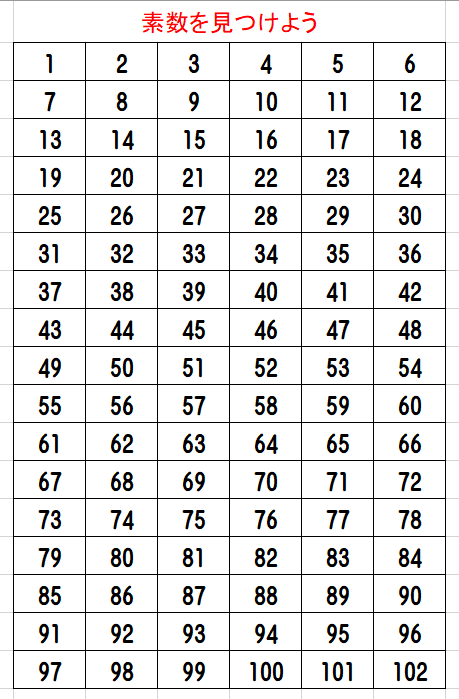
- 数字の一覧表を作る(1~6までが一行目になるようにすると良い)。
- 1は素数ではないので×をつける。
- 2は素数なので2を○で囲む。2の倍数をマーカーペンで消していく。上の表の場合は,2と4と6の列が消えることになる。
- 3は素数なので3を○で囲む。3の倍数を違う色のマーカーペンで消していく。上の表の場合は,3と6の列が消えることになる(6の列はすでに消えている。これは2と3の公倍数だ)。
- 以下,同じようにやっていく。
- 13以降,残っている数字は,すべて素数なのでその数字を○で囲むだけでもいいが,初めてのときはじっくり倍数を消していくのがいい。
PowerPointで作成(動画とPP用file)
エラストテネスとは(Wikipediaより)
エラトステネス(Ερατοσθένης, Eratosthenes, 紀元前275年 – 紀元前194年)は、ヘレニズム時代のエジプトで活躍したギリシャ人の学者であり、アレクサンドリア図書館を含む研究機関であるムセイオンの館長を務めた。業績は文献学、地理学をはじめヘレニズム時代の学問の多岐に渡るが、特に数学と天文学の分野で後世に残る大きな業績を残した。
地球の大きさを初めて測定した人物として、また素数の判定法であるエラトステネスの篩を発明したことで知られる。その業績から「第2のプラトン」とも呼ばれた。また「β」(ベータ)ともあだ名されている。その由来は、「世界で2番目に物事をよく知っている人」という意味である。(下線は引用者)




コメント
≪…エラトステネスの篩…≫を、『幻のマスキングテープ』の[でんぐり返し]で調べる方法があるとか・・・
数の言葉ヒフミヨ(1234)が、あらゆる現象を説明しうる数学の基の自然数には、[素数]に偶力が潜んでいるらしい・・・
[進み行く素数]=[ある既素数]+[ある既素数]-[1]
の光景が令和6年4月に開設の岡潔数学体験館で観られるといいなぁ~